こんにちは。うめおにぎりです。
この記事では、的玉の狙う場所について考察していきます。
「ビリヤードでイメージがわかない」「イメージどうりなのになぜか入らないという悩みはないでしょうか?」
高校までの数学で考察していきたいなと思います。
ビリヤード狙い方
①イメージボール ②接点 ③厚み など、いろいろな狙い方がありますが、ここでは③厚みで狙うのを考えようかなと思います。
私自身、ビリヤード初心者でうまく入らないことが多いので、どこを狙えばどの角度で飛んでいくのかが③厚みが一番わかりやすいかなと思います。
①イメージボール ②接点 とかは球のどこにあたるのかを想像しないといけないですが、球は球体なのでどうしても角度とかがついたりすると、どこを狙えばいいかわからなくなります。球の奥行も含めてみないといけないので初心者の私には難しいと感じました。
厚みの考察
どれぐらいの厚みで衝突すれば、どのような角度で進むのかの考察をしていきます。
例えば、手玉の中心が的球の中心に当たると直線に進みます。これは当たり前ですね。
このときの厚みはすべて重なっているので1とします。
図1
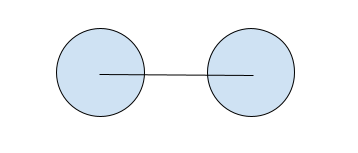
図1は的玉と手玉の中心を結んでいます。次からは、的玉と、手玉の中心がずれた場合について考えていきます。
球同士が衝突すると、接線に対して垂直方向に力が伝わります。
図2
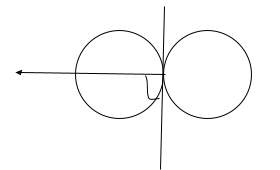
すなわち、この接線に対して垂直方向に的玉が進む形になります。
具体例で考える:30度に飛ばしたいとき
的玉を進行方向に対して30度に進ませたいとき、的玉のどの場所に手玉を衝突させればよいのかを考えていきます。
図3
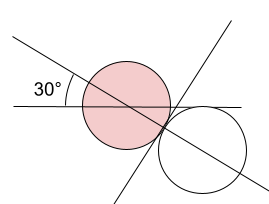
赤球:的玉 白玉:イメージボール
的玉とイメージボールの中心を結んだ線と的玉の横の線のなす角が30度になれば、的玉は30度の角度で進むことが分かります。
この時の厚みを計算してみようと思います。
ビリヤード球の直径:57mmとすると、的玉と手玉の中心を結んだ長さは28.5mm × 2 = 57mm
図4
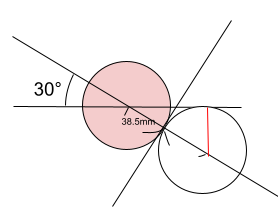
このとき赤線(的玉の中心をとおる横の線とイメージボールの中心を垂直に結ぶ線)の長さを求めます。
高校での三角比(sin, cos, tan)を用いれば求めることができます。
赤線 = 的玉と手玉の中心を結んだ長さ × sin30°
すなわち、28.5 × 2 × 1/2 = 28.5
ここで厚みを計算します。簡単に言えばイメージボールがどれだけ的玉に重なっているかです。
図5

的玉の直径57mmにたいして、イメージボールが28.5mm重なっているので
厚みは 28.5mm / 57mm = 1/2 となります。
これは手玉の中心を的玉のちょうど端と結んだラインを狙うと、的玉は30°で進んでいくことになります。
30度の狙い方:結論
厚み 1/2で狙えば30°で進む。このとき狙う場所は、手玉の中心から的玉のちょうど端、イメージボールと的玉がちょうど半分重なるようにねらえばいいです。
厚みの一般化
30°以外の場合も考えます。
球の直径:r として考えると
図6
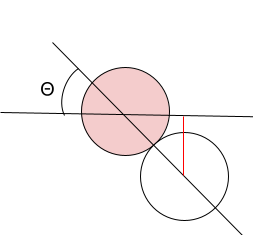
赤線 = 的玉とイメージボールの中心を結んだ線 × sinΘ
赤線 = r × sinΘ
図7
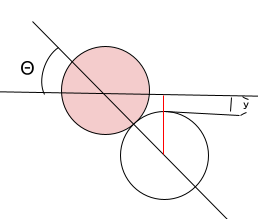
ここでy(イメージボールから的玉の中心を通る横線の最短距離)を求めます。
y = 赤線 – 球の半径
y = r × sinΘ – 1/2r
図8
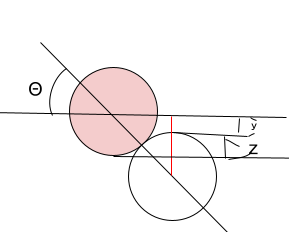
z(的玉とイメージボールの重なってる距離)を求めます。
z = 球の半径 – y
すなわち z = 1/2r – (r × sinΘ – 1/2r)
z = r(1 – sinΘ)
ここで的玉とイメージボールの厚みを計算すると
図9
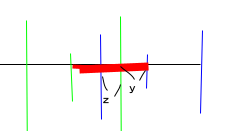
緑線:イメージボール 青線:的玉
的玉とイメージボールの重なってる距離は図9より、zです。
的玉の直径rに対して、zだけかさなっているので、厚みは
厚み = z / r
厚み = r(1 – sinΘ) / r
厚み = 1 – sinΘ となります。
厚みの結論
以上のことから厚みは「1 – sinΘ」で求めることができるとわかりました。
これをグラフにするとこのような感じになりました。
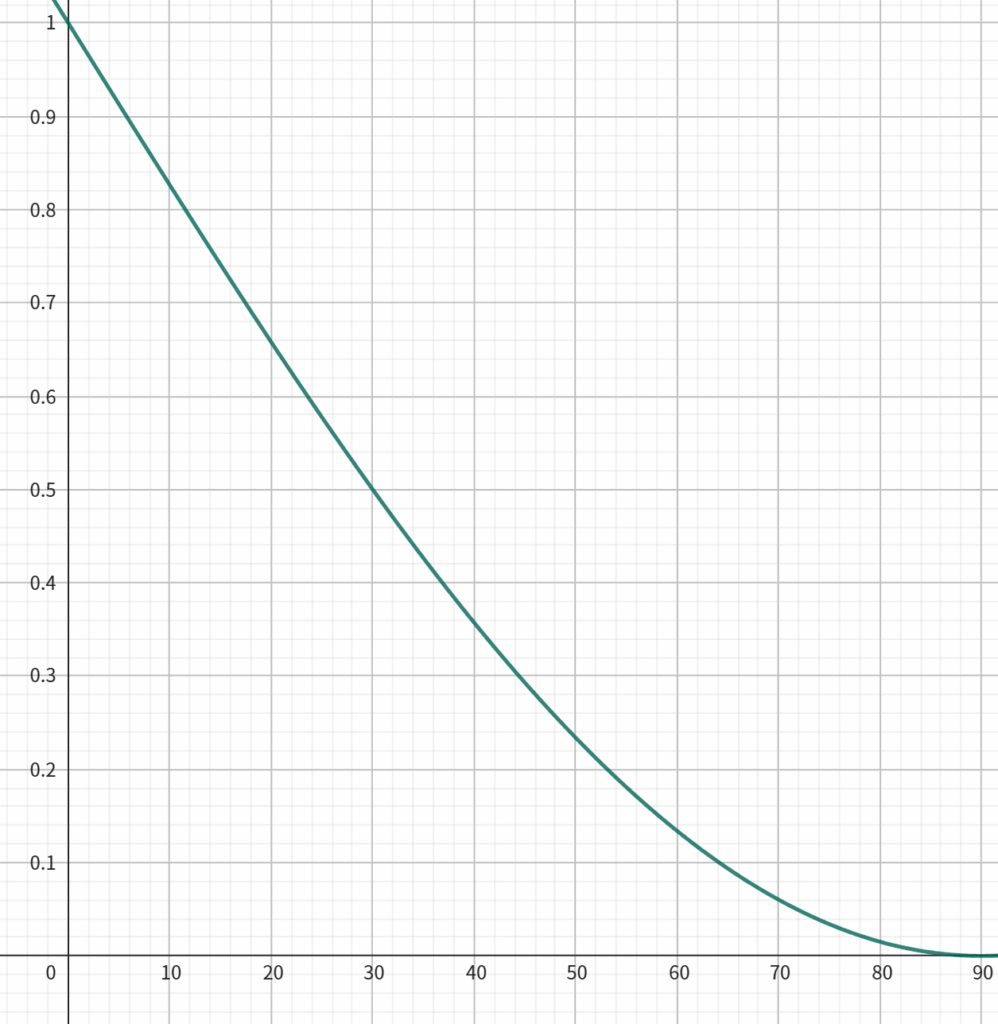
総評
以外とシンプルに計算はできたが、実際には球速や回転、摩擦などの影響によりこのようにいかないことが多々あります。これからは、その球速による違いなどによる軌道の変化などを考えたいが、これらはただ計算してみたに過ぎないので、実際にプレイするのが一番上達には早いと思います。しかし、始めたばかりだとイメージすらわかないので、なんとなくの目安にはなるのかなと、これからの練習で感覚を身につけたいと思います。

